Geni indefor matematik? {{forumTopicSubject}}

Hej alle

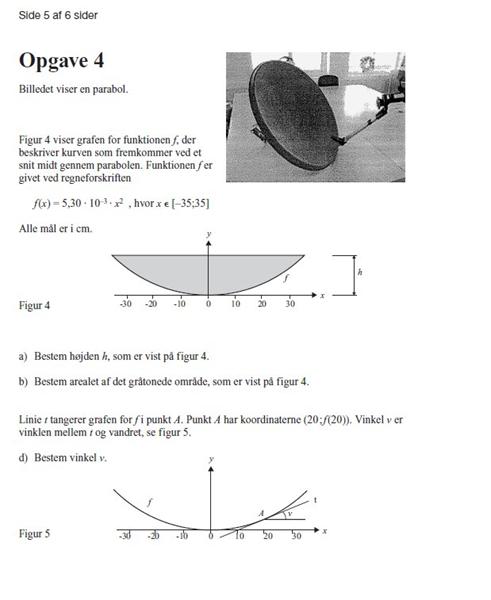
er der nogle som er gode til matematik? Hvis ja ville det være rigtig dejligt, hvis I kunne forklare mig hvad man skal gøre i følgende opgave: (Det er hele opgaven jeg ikke forstår)

På forhånd tak

Se svar (8) >>

Spar penge på din forsikring

Gå til sidste svar

Kommentarer på: Geni indefor matematik?

Amalie :) . Tilmeldt:
nov 2008
Følger: 69 Følgere: 65 Heste: 4 Svar: 2.349

#1 11. jan 2015 Højden kan du finde således:
Du skal finde afstanden mellem punktet (35,0) og punktet (35,f(35). Der skal du jo sådan set bare finde ud af hvad f(35) er, og så har du højden
Amalie :) . Tilmeldt:
nov 2008
Følger: 69 Følgere: 65 Heste: 4 Svar: 2.349

#2 11. jan 2015 Nr. 2 er jeg ikke helt sikker på.. Der ville jeg nok finde integralet, og så efterfølgende arealet af "det hele" (70 * h).. Så jeg ville nok sige
A = (70*h)-integralet
Kathrine L Tilmeldt:
mar 2013
Følger: 18 Følgere: 16 Heste: 1 Emner: 33 Svar: 388

#3 11. jan 2015 Amalie :): men hvordan finder man integralet?
Amalie :) . Tilmeldt:
nov 2008
Følger: 69 Følgere: 65 Heste: 4 Svar: 2.349

#4 11. jan 2015 Du finder arealet under grafen. Det gøres ved at finde stamfunktioner. Hvis I ikke har arbejdet med det endnu, er det måske ikke sådan, din lærer mener, at du skal gribe opgaven an
C Tilmeldt:
feb 2009
Følger: 69 Følgere: 65 Heste: 5 Emner: 49 Svar: 428

#5 11. jan 2015 I opgave a: sætter du f(0) da du derved finder y værdien som er din højde.
I opgave b: interegere du over området -35 og 35 for fomlen og derved kommer arealet.
Den sidste opgave er noget med tangenthældning og vinkler, slå det op i matematikbogen, den kan jeg ikke lige på stående fod
Amalie :) . Tilmeldt:
nov 2008
Følger: 69 Følgere: 65 Heste: 4 Svar: 2.349

#6 11. jan 2015 Charlotte: Hun skal da ikke tage f(0)... Så får hun i hvert fald ikke højden! Hun bliver nødt til at tage f(35) eller f(-35)
C Tilmeldt:
feb 2009
Følger: 69 Følgere: 65 Heste: 5 Emner: 49 Svar: 428

#7 14. jan 2015 Højden vil være den samme, da den streg er vandret og dermed er det nemmest at finde højden ved 0 for at kontrollere langs y aksen.
Hønen Tilmeldt:
maj 2008
Følger: 20 Følgere: 24 Heste: 1 Emner: 203 Svar: 3.460

#8 14. jan 2015 Højden ved 0 er 0 Da f(0) = 0
Så det er f(-35) eller f(35) der skal bruges.

b, der skal du bruge integralet. vær dog opmærksom på, at den regner integralet under kurven, derfor skal du regne arealet af det rektangel figuren er inden for, og trække integralet fra.

c: er noget med tangentens hældning i forhold til x-aksen. Jeg kan ikke lige huske den nøjagtige måde at regne det på og jeg kan ikke nå at tænke mig nok om

Gå til toppen

Kommentér på:
Geni indefor matematik?

Annonce

{{ group.groupName }}

Geni indefor matematik? {{forumTopicSubject}}